|
网络上,在遇到很有内涵的内容的时候,人们往往会说“这条微博信息量真大”。从古至今,人们一直在试图找到一种衡量消息中“信息浓度”的方法。例如,我们很容易得出结论,对于一名 NBA 球迷来说“总冠军是小牛队”所蕴含的信息量比“总冠军是一支西部球队”大,但是要比较“本文作者是男生”和“本文作者是单身”这两条信息所蕴含的内容多少可就有点强人所难。在大多数语言中,“信息”一词往往以不可数的形式出现,这也从另一方面印证了这一问题的困难程度。 到了信息时代,对信号的处理与分析又需要一个适当的对信息量的衡量标准,所以数学家们也被这一问题困扰着。直到1948年,这个问题被香农在论文《通信的数学理论》中首次解决,这才让数学家们松了一口气。 香农公理和信息熵信息就是使我们了解到的事物未知的性质,如果换成物理学家惯用的说法就是信息是对事件进行观测的结果。对于未知的事物,我们的观测存在着很多种可能的结果,而得到这些结果的可能性是不同的。换句话说,信息的作用就体现在使得某事件发生的概率从之前的某个概率变为1。所以信息量是与概率有关的。基于此,香农提出了他的第一条假设:信息量是关于事件发生概率的函数。同时为了方便起见,香农还规定这一函数连续。 除此之外,香农还提出其他 3 条假设,综合起来就是有名香农公理:
- 信息量是关于事件发生概率的连续函数;
- 如果两事件A与B,B是A的必要条件,那么获知事件A要发生所对应的信息所含的信息量要大于或等于获知事件B要发生所对应的信息所含的信息量;
- 获知独立事件将同时发生的信息量应为单独获知两事件发生的信息量之和;
- 任何信息的信息量都是有界的。
基于公理1,我们定义获知时间 A 发生这条信息的信息量为I(A)=f(p(A))。又由公理2,在这一情况下p(A)
我们先做代换取q=lnp,则:
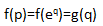
那么:
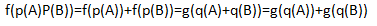
而由于f(p)连续,则g(q)也连续,可以证明,在连续的条件下惟一的解是g(q)=cq,代入最初的方程有:
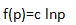
这就是信息量的数学定义,在使用中我们常取c=-log2e,则f(p)=-log2p,这就是著名的“比特”。当然在某一次试验之前我们并不能确知试验的结果,那么这一试验可能获得的信息量的期望是:
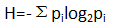
由于这一公式的形式非常类似物理中“熵”的定义,香农把这一平均信息量称为“信息熵”。由函数的性质可知,当各种结果出现的概率均等时,此次试验能获得的信息量的期望最大。
信息熵的应用信息熵的应用很广,即便是在智力题里也有体现:有 100 个外表相同的球,已知其中有一个与其他球的质量不同。现要求用没有砝码的天平在最少次数中找出这个球,问怎样的称法才是最佳的? 我们把每次称量都视为一次试验,试验结果有三种:天平偏向左边、天平偏向右边重或者相等,那么为获得最大的信息量,我们应该使三种情况出现的概率相等,即把小球平均分成 3 份进行称量,也就是一般答案中给出的最佳称量方法。使用信息论还可以计算出最少所需要的称量次数,因为100个小球中知道某球是假球且偏重或者偏轻这一信息所包含的信息量是 log 2 200,每次测量所能获得的信息是 log 2 3,那么需要测量的最小次数就是 5 次。然而具体到每次测量,由于不能保证将球平均分为 3 份,并不一定能有 log 2 3 的信息熵,所以这个 5 次只是测量的下界,具体能否达到还要看实际的步骤。 也有学者把信息熵的理论应用在语言学上,他们统计了不同语言中各字母的频率,英语的平均信息熵是 4.03 比特,法语的平均信息熵是 3.98,西班牙语是 4.01 比特,德语的是 4.10 比特,俄文的是 4.8 比特,都略低于相应字符集的最大信息熵。这也是很容易理解的,自然语言中存在许多词首词尾与固定搭配,不同字母的出现频率是不同的。但是信息学家们并不满意这个结果,因为在传输中更大的平均信息熵就意味着更高的效率,所以他们一直在试图追寻能使信息熵更高的压缩编码方式,像我们常用的WinRAR等软件就是他们工作的结果。当然,这样的“理想语言“在人类眼中看来是毫无文采、索然无趣的。我们使用的自然语言中正是由于那么一点多余的低效率,才造出了丰富多彩的效果。另外值得一提的是,中文的信息熵高达 9.65 比特,也许这也是汉语中各种文字游戏比较多的根源吧。有的家长会给孩子起个带生僻字的名字,其实也在无形中稍微提高了汉语的效率呢。
| 













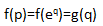
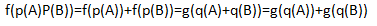
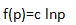
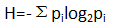
 提升卡
提升卡 置顶卡
置顶卡 沉默卡
沉默卡 喧嚣卡
喧嚣卡 变色卡
变色卡 千斤顶
千斤顶 显身卡
显身卡